Boekbespreking: Conquest of the Plane, 
door Jeroen Spandaw, Euclides, 
blad voor leraren wiskunde, Februari 2012, 87-4, 
p168-170. 

Dit is pagina 170. Zie 168 of 169.

Stapgewijs commentaar bij deze "bespreking" door Thomas Colignatus, 13 februari 2012, in aanvulling op de samenvattende reactie.

Dit is pagina 170. Zie 168 of 169.

Dus verkeerd 
weergegeven (V)
of lasterlijk (L)

1. Spandaw trekt dit in welles-nietes waarbij hij alleen verwijst naar de traditionele aanpak en mijn kritiek niet noemt:
2. Overly complex, want: (a) gebruik van limiet concept terwijl dat niet nodig is, (b) het algebraisch vereenvoudigen wordt impliciet gebruikt voor het bepalen van de limietwaarde
3. Essentially inconsistent: (a) gezegd wordt dat het differentiequotient niet gedefinieerd is maar vervolgens wordt een waarde toegevoegd, en je kunt die waarde ook vinden door expliciet algebraisch te vereenvoudigen, (b) voor iedere epsilon en delta heb je weer een epsilon' en delta' nodig om te bewijzen dat ook zij echt continue zijn. 

1. De aanhalingstekens krijgen bij de lezer plausibiliteit omdat Spandaw niet mijn werkelijke ontdekking noemt maar de onbenulligheid dat bij deling een term kan wegvallen. Sukkel ontdekt dat hij een boer kan laten, zoiets.
2. De echte ontdekking is het verschil tussen statische deling (resultaat) en dynamische deling (proces met manipulatie van het domein), met vervolgens de uitwerking naar afgeleide en integraal, inclusief herkenning van deze begrippen als algebra, met continuiteit in termen van formule. Dus een complexer geheel. 

1. Numerieke continuiteit is niet het enige criterium voor "wiskundige" juistheid. Dit is misbruik van het woord "wiskundig". Ja, het is traditioneel denken volgens Weierstraß maar algebra is ook onderdeel van de wiskunde.
2. Spandaw zou ook de staf breken over de huidige schoolwiskunde, die niet naar continuiteit kijkt.
3. Hij ziet dus niet dat de algebraische aanpak een kader biedt voor een consistente aanpak van analyse voor school, zonder tierlantijnen die hierboven zijn genoemd.
4. Hij vermeldt niet dat COTP expliciet stelt dat vraagstukken van continuiteit tot een ander discussiedomein behoren (bijv. het college analyse voor eerstejaars studenten wiskunde).

1. Dit is niet het didactisch tovermiddel.
2. Er is geen wiskundige ontdekking t.a.v. de verkeerde voorstelling door Spandaw.
3. Er is wel degelijk een wiskundige ontdekking zoals hierboven genoemd:  het verschil tussen statische deling (resultaat) en dynamische deling (proces met manipulatie van het domein), met vervolgens de uitwerking naar afgeleide en integraal, inclusief herkenning van deze begrippen als algebra, met continuiteit in termen van formule. Dus een complexer geheel.
4. Ook "lim h -> 0" blijkt overbodig.
5. Ik ben geen wiskundige pur sang en voor mij lag daar geen uitdaging in het formuleren van een andere aanpak voor de afgeleide. Wel constateerde ik dat het voor het onderwijs en voor de leerlingen lastig is om almaar "lim h ->  0" erbij te schrijven en ook op het juiste moment daarmee op te houden. Het is ballast zonder extra inzicht. Ik had altijd al argwaan tegen Weierstraß's gekronkel in de predicatenlogica en gebrek aan elegantie. Bij het hertypen van ALOE in 2007 leek het logisch ook naar de paradoxen bij het delen door nul te kijken. De algebraische formulering van de afgeleide rolde er als een bijproduct uit. COTP presenteert het in een geïntegreerd kader. Commentaar van anderen is welkom om misverstanden weg te nemen en e.e.a. op te poetsen. Maar het lijkt me nu al een resultaat voor de mathesis.

1. Dit is volstrekt onwaar. De algebraische aanpak van de afgeleide (COTP) kun je niet gelijkstellen aan het ontwikkelen van een algebra die ook van toepassing is op de afgeleide ('Derivation'). 
2. De aanpak van COTP staat vandaag niet in wikipedia. 
3. Wat COTP doet is wel degelijk een originele en nieuwe formulering - totdat historisch onderzoek laat zien dat iemand anders al eens eerder is ondergesneeuwd.

1. COTP legt uit dat hier logica wordt gebruikt. Spandaw laat niet zien dat dit gebruik van logica onhoudbaar is. 
2. Als je wilt kun je overal limieten in hangen, ook met lichtjes in de kerstboom, maar dat is geen argument dat ze nodig zijn wanneer ook logica volstaat.
3. De suggestie dat ik hier niet consistent ben is lasterlijk. Men kan denken dat ik dan te gevoelig ben voor kritiek en dat een recensent de vrijheid heeft om interpretatiefouten en dergelijke te maken, maar, ik heb juist met zorg ernaar gekeken dat de aanpak consistent bleef. De aanpak van de afgeleiden van de goniometrische functies is geen sinecure. Als ik deze aanpak niet had gevonden, dus wanneer ik niet had geconstateerd dat logica volstaat, dan had ik inderdaad de conclusie getrokken dat limieten nodig zijn (in afwachting van een alternatief). Dus dit is geen eenvoudig verschil van inzicht of een kwestie van overgevoeligheid van mijn kant maar een kernkwestie.

1. Dus wel.

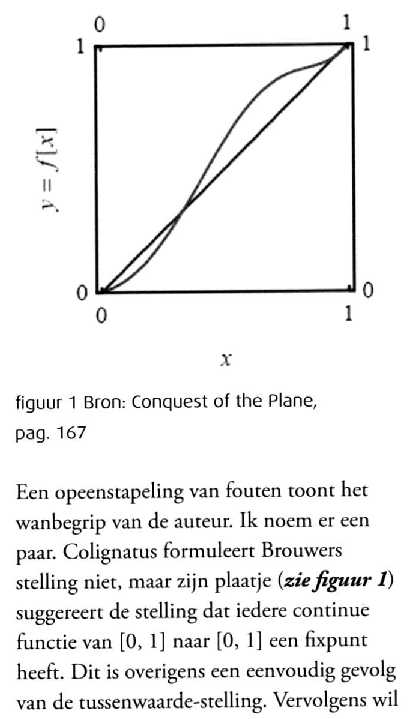
1. COTP introduceert het getal e met het didactisch voorbeeld van Brouwer's fixed point. Het is slechts een didactisch opstapje, met als pluspunt dat de dekpuntstelling genoemd wordt. Het lijkt me een elegante introductie die meteen de essentie weergeeft: de afgeleide van Exp[x] is weer Exp[x]. 
2. Er wordt geen poging gedaan om een functieruimte te bouwen, Bouwer's stelling te bewijzen of wat ook, en er wordt gezegd dat we dit niet doen, en dat het alleen een didactisch opstapje is. 

1. Spandaw verlangt echter dat het helemaal uitgewerkt wordt. Ik acht dat een dubieus verlangen want wellicht hebben eerst Exp[x] nodig voordat we dat kunnen doen. Het is slechts een didactisch opstapje, en dat wordt ook letterlijk zo uitgelegd.
2. Overigens laat ik de functie in de oorsprong beginnen en in {1, 1} eindigen zodat het ook triviaal wordt, maar voor de leerlingen wel gemakkelijker te controleren.
3. Lasterlijk: fouten en wanbegrip.

1. Spandaw meent dat er een betere didactische introductie is. Fijn, er zijn diverse leerboeken wiskunde die verschillende wijzen van introductie hebben die de auteurs van die boeken ongetwijfeld allemaal didactisch beter vinden. Echter, mijn visie is dat we niet zomaar kunnen zeggen wat echt beter is zonder dat we naar de empirie kijken wat leerlingen echt snel oppakken en wat langer blijft hangen. 
2. Spandaw's stelling is ex cathedra: "Je kunt eenvoudig aannemelijk maken ..."  Onzin, wat je aannemelijk kunt maken is een empirische didactische kwestie en niet iets waarvan een traditioneel opgeleid wiskundige denkt dat het aannemelijk is. 
3. Vervolgens zit Spandaw in het keurslijf van de limieten terwijl COTP de stap naar de algebraische aanpak maakt, wat een andere didactiek dan de traditionele leerboeken kan verlangen. In de didactische aanpak van COTP wordt eerst de essentie van Exp[x] gegeven en vervolgens besproken wat dit voor de algebra betekent.
4. Spandaw ziet dit allemaal niet. Het staat er allemaal maar hij ziet het niet want hij denkt traditioneel en blijkt blind.
5. Je kunt met f' = f het leerstuk van de differentiaalvergelijkingen aansnijden maar dat doet COTP niet. Spandaw kiest een te complexe formulering voor wat het doel van het didactische opstapje is.

1. De nette uitwerking op de algebraische methode staat in paragraaf 12.1.8.3. op pag 173.

1. Tendentieus: vele paginas, wiskundige missers, wiskundig tekort schieten

1. COTP beargumenteert dat het een misvatting is dat de radiaal een 'dimensieloos' getal is, zogenaamd van afstand / afstand, omdat bij wegdelen nog een factor "rondom" overblijft.
2. Die blikwisseling bij Pythagoras lijkt me overigens belangrijk voor het begrijpen van Pythagoras terwijl het m.i. zelden genoemd wordt.

1. COTP begrijpt heel goed dat wiskundigen dit denken.
2. COTP heeft argumenten aangedragen om er anders tegen aan te kijken.

1. Een denkelijk acceptabele formulering voor een recensent die de balans opmaakt.

1. In principe heeft een recensent de vrijheid om te oordelen dat ergens slechte wiskunde zou zijn. Maar dat moet dan wel onderbouwd zijn. Spandaw meent die onderbouwing te hebben gegeven, maar we hebben boven gezien dat hij de zaken verkeerd voorstelt, niet mijn analyse weergeeft maar zelf wat interpreteert, en dat hij blind is voor betere wiskunde.
2. COTP hoofdstuk 16 geeft het overzicht van "The News", wat dus niet in die andere bronnen is te vinden. Spandaw mag daar blij mee zijn maar de bedoeling van een "bespreking" is dat lezers een beeld van dat nieuws hebben.
3. Spandaw noemt niet de PDF terwijl de andere boeken blijkbaar achter tariefmuren zitten.
4. Alleen de traditionele aanpak van de analyse wordt "correct" genoemd terwijl de algebarische aanpak tot dezelfde uitkomsten leidt, en dan niet deugt ? Zou het echt toeval zijn dat er voor de functies of school systematisch hetzelfde uitkomt ? Maar na indoctrinatie heeft de traditionele wiskundige afgeleerd feiten te zien en nieuwsgierig te zijn.
5. Lasterlijk: slechte wiskunde, hilarisch, pseudo-wiskunde.
6. Lasterlijk: geschrijf (ook generaliserend)